Teoremas de las funciones continuas

Las funciones que son continuas en un intervalo cerrado tienen ciertas propiedades especiales que se enuncian a continuación:
Teorema de Bolzano (o de los ceros):
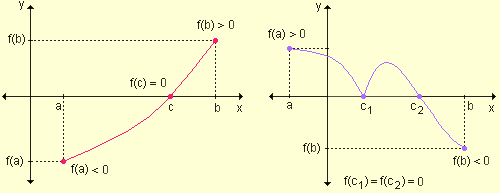
Si y = f(x) es una función continua en el intervalo cerrado [a, b] y f(a) y f(b) tienen signos opuestos, entonces existe al menos un número real c perteneciente al intervalo (a, b) tal que f(c) = 0; es decir, c es una raíz de f(x).
Las siguientes gráficas permiten ilustrar el teorema:
Propiedad de Darboux (del valor intermedio)
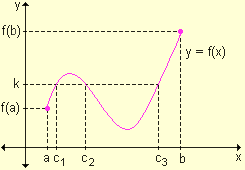
Si y = f(x) es una función continua en el intervalo cerrado [a, b] donde f(a) ¹ f(b) y k es un número real cualquiera comprendido entre f(a) y f(b), existe al menos un número real c perteneciente al intervalo (a, b) tal que f(c) = k.
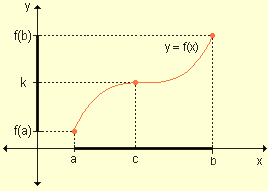
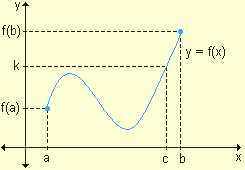
Desde el punto de vista geométrico, este teorema establece que la gráfica de una función continua en un intervalo cerrado, debe intersecar al menos una vez a cada recta de ecuación y = k, siendo f(a) < k < f(b).
Teorema de Rolle
Si f es una función continua definida en un intervalo cerrado [a,b] , derivable sobre el intervalo abierto (a,b) y f (a) = a f(b) , entonces:
Existe al menos un punto C perteneciente al intervalo (a,b) tal que f' (C)=0 .
Si una función es:
Continua en [a, b]
Derivable en (a, b)
Y si f(a) = f(b)
Entonces, existe algún punto c (a, b) en el que f'(c) = 0.
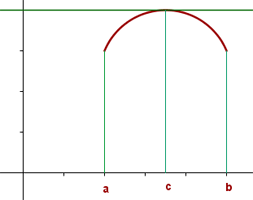
La interpretación gráfica del teorema de Rolle nos dice que hay un punto en el que la tangente es paralela al eje de abscisas.