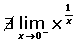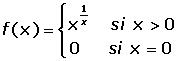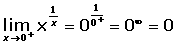Algunas soluciones:

1.
La función es continua en todos los puntos de su dominio.
D = R− {−2,2}
La función tiene dos puntos de discontinuidad en x = −2 y x = 2.
La función es continua en toda R menos en los valores que se anula el denominador, si igualamos éste a cero y resolvemos la ecuación obtendremos los puntos de discontinuidad.
x = −3; y resolviendo la ecuación de 2º grado obtenemos también: x=2−√3 y x=2+√3
La función tiene tres puntos de discontinuidad en x=−3, x=2−√3 y x=2+√3
2.
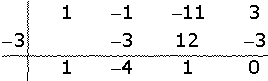
3.
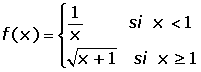
En x = 1 hay una discontinuidad de salto finito
4.
Determina si la función valor absoluto es continua en el punto cero.
Su grafico es :

4.
Sabemos que por definición la función valor absoluto esta definido como:
Como podemos ver la función no esta definida en el punto x=0, desde su definición la función no existe en ese punto. Por lo tanto la función en x=0 no es continua.
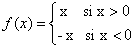
5.
Hallar los x interseptos de la función x^2 - 8x + 15 luego encontrar los valores del teorema de Rolle tal que f'(x) sea igual a 0
f(a) = f(b) = 0
Entonces, existe algún punto c (a, b) en el que f'(c) = 0.
Los x intersectos vienen dados por:
x^2 - 8x + 15
(x - 3) (x - 5)
x = 3
x = 5
[3 , 5]
Para hallar el valor de se deriva y luego se despeja:
x^2 - 8x + 15 = 0
2x - 8 = 0
2x = 8
x = 8/2
x = 4
Sustituyendo el valor de x en la formula original obtenemos:
f(4)= x^2 - 8x + 15
= 4^2 - 8*4 +15
= 16 - 32 +15
= -1
Estudia la continuidad de f(x) en x = 0.
f(0)=0
En x = 0 hay una discontinuidad esencial.
6.